数组实现树结构

在本课程中，涉及二叉树甚至多叉树的题目用指针确实都可以做，但考虑到大家对指针掌握程度有限；使用指针时容易出现各种内存问题；即使不出现内存问题，使用指针的程序在调试时也会非常不方便。因此，在此给出用数组实现树的 demo，方便大家做题：

定义二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#define TREE_SIZE 1000 // 最大节点数  
int left[TREE_SIZE], right[TREE_SIZE]; // 存左右子节点编号
int values[TREE_SIZE]; // 存每个节点的值

const int root = 1; // 根节点编号固定为1
int cnt = 0; // 当前节点总数（编号最大值）

// 创建一棵新树
void newtree(int value)
{
  left[root] = right[root] = 0; // 初始化左右子树为空
  values[root] = value; // 给根节点赋值
  cnt = root; // 当前只有根节点
}

// 创建新节点
int newnode(int value)
{
  int u = ++cnt; // 新节点编号
  left[u] = right[u] = 0; // 初始化左右子节点为空
  values[u] = value; // 给节点赋值
  return u; // 返回这个节点编号
}

定义多叉树

方法与定义二叉树基本一致，只是将索引树的数组从 left、right 变成更高维。

假设要定义一棵 5 叉树：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#define TREE_SIZE 1000
int next[TREE_SIZE][5]; // 每个节点最多有5个子节点
int values[TREE_SIZE]; // 节点的值
const int root = 1;
int cnt = 0;

// 创建一棵新树
void newtree(int value)
{
  for (int i = 0; i < 5; i++)
  {
    next[root][i] = 0; // 所有子节点初始化为0（空）
  }
  values[root] = value;
  cnt = root;
}

int newnode(int value)
{
  int u = ++cnt;
  for (int i = 0; i < 5; i++)
  {
    next[u][i] = 0; // 初始化5个子节点为空
  }
  values[u] = value;
  return u;
}

具体例子

光看方法可能比较抽象，下面结合一道题目具体看看如何用数组来解树的题目：

【问题描述】

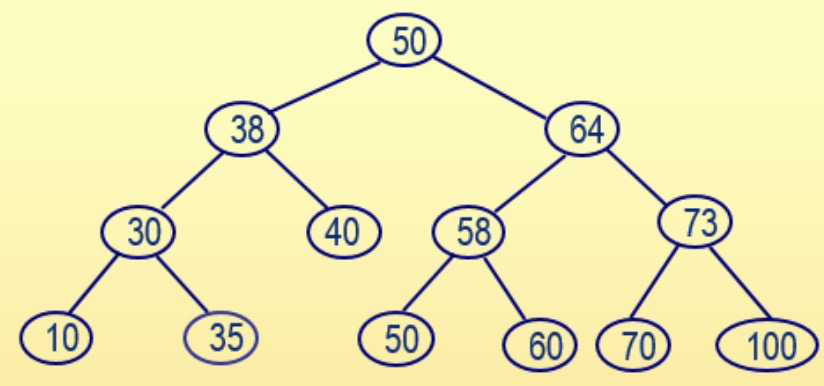
从标准输入中输入一组整数，在输入过程中按照左子结点值小于根结点值、右子结点值大于等于根结点值的方式构造一棵二叉查找树，然后从左至右输出所有树中叶结点的值及高度（根结点的高度为1）。例如，若按照以下顺序输入一组整数：50、38、30、64、58、40、10、73、70、50、60、100、35，则生成下面的二叉查找树：

image-20250424165038608

从左到右的叶子结点包括：10、35、40、50、60、70、100，叶结点40的高度为3，其它叶结点的高度都为4。

【输入形式】

先从标准输入读取整数的个数，然后从下一行开始输入各个整数，整数之间以一个空格分隔。
【输出形式】

按照从左到右的顺序分行输出叶结点的值及高度，值和高度之间以一个空格分隔。
【样例输入】

13

50 38 30 64 58 40 10 73 70 50 60 100 35
【样例输出】

10 4

35 4

40 3

50 4

60 4

70 4

100 4

【样例说明】

按照从左到右的顺序输出叶结点（即没有子树的结点）的值和高度，每行输出一个。

示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <stdio.h>

// 全局变量初始化
int id = 1;         // 用于生成新节点的编号
int root = 1;       // 根节点编号固定为1
int left[1000];     // left[i] 表示编号为i的节点的左子节点编号
int right[1000];    // right[i] 表示编号为i的节点的右子节点编号
int value[1000];    // value[i] 表示编号为i的节点存储的值

// 创建一个新节点，值为x，返回该节点的编号
int create_new_node(int x)
{
    int u = ++id;              // 创建新节点编号
    left[u] = right[u] = 0;    // 初始化新节点的左右孩子为0（即空）
    value[u] = x;              // 设置节点的值
    return u;                  // 返回新节点编号
}

// 中序遍历，参数 tree 是当前节点编号，x 是当前节点的层数（根为1）
void inorder(int tree, int x)
{
    if (!tree)                 // 如果当前节点为空（0），直接返回
        return;

    inorder(left[tree], x + 1);  // 递归遍历左子树，层数+1

    // 如果是叶子节点（没有左右子树），输出值和层数
    if (left[tree] == 0 && right[tree] == 0)
    {
        printf("%d %d\n", value[tree], x); // 打印叶子节点的值 和 所在层数
    }

    inorder(right[tree], x + 1); // 递归遍历右子树，层数+1
}

int main()
{
    int n;
    scanf("%d", &n); // 读取节点个数
    n--;             // 第一个值用作根节点，剩下的插入

    int temp;
    scanf("%d", &temp);          // 读取根节点的值
    left[root] = right[root] = 0; // 初始化根节点的左右子树为空
    value[root] = temp;           // 设置根节点值

    // 插入剩余 n 个节点
    while (n--)
    {
        scanf("%d", &temp); // 读取要插入的值
        int p = root;       // 从根节点开始查找插入位置

        while (1)
        {
            if (temp < value[p]) // 如果插入值比当前节点小，往左走
            {
                if (left[p] == 0) // 如果左子节点为空，插入到这里
                {
                    left[p] = create_new_node(temp);
                    break;
                }
                else
                    p = left[p]; // 否则继续向左走
            }
            else // 插入值 >= 当前值，往右走
            {
                if (right[p] == 0) // 如果右子节点为空，插入到这里
                {
                    right[p] = create_new_node(temp);
                    break;
                }
                else
                    p = right[p]; // 否则继续向右走
            }
        }
    }

    // 中序遍历整棵树，输出所有叶子节点的值和层数
    inorder(root, 1);

    return 0;
}